How does the S/N ratio compare when using chop-nod vs. quad chopping? Four images are taken in each case; call them A, B, C, and D. Assume that in the chop-nod frames the star is centered on the same pixels in the detector for two of the positions (A and D), and in the quad chopping all four images contain the star, but in different parts of the detector.

First, for chop-nod:

The final frame will be of the form (A-B) - (C-D) = A + D - B - C.
A-B and C-D both have the sky removed from them, but have residual radiative offsets. The difference between them (i.e. the final frame) has both sky and radiative offset removed.

The total signal is measured from a single box on the final frame, and gives 2*I where I is the total signal and sqrt(4*B) is the background noise (assuming that the background noise dominates).

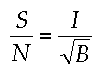
Second, for quad chopping:

The final frame is still (A-B) - (C-D) = A + D - B - C.
However, in order to sum the four images either four copies of the final image must be shifted into register and added together, or the S/N must be calculated for each individual image and then the final S/N calculated.

Any given image will have a signal of I. The noise will be sqrt(4*B). Hence there will be four images, each with a signal-to-noise ratio of I/sqrt(4*B).

The sum of the signals is 4*I. The quadrature sum of the noise will be sqrt(4*4*B) = 4*sqrt(B). Hence the final signal-to-noise ratio is:

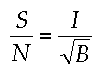
The signal-to-noise ratio of chop-nod image sets is the same as for quad chopping images sets, in spite of the latter having twice as many images! This somewhat counterintuitive result stems from the fact that noise from four different regions of the detector must be combined in quad chopping.

Third, for chop-nod on chip:

If the field size is at least three time as large as the object, you may be able to perform a chop-nod sequence with all three positions on the detector. This can only give a higher S/N than chop-nod in which two of the positions are not recorded on the chip. The extra signal from each outer position is I, while the noise is sqrt(B). Adding all three positions gives S=4*I, while N=sqrt(3*4*B), hence

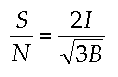
This is 2/sqrt(3) = 1.16 times better S/N than either of the other techniques. While it takes the most detector real estate of all the techniques this may be the best to use for point sources.

Other factors

There are some other factors to consider:

1. Systematic or fixed-pattern noise on the detectors can be averaged out by "dithering" the image from one part of the detector to another. Quad chopping does this automatically, while chop-nod requires (for the same S/N) that the star images fall on the same part of the detector. Hence fixed pattern noise will be a factor of two less in quad-chopping, if done carefully.
2. Image overlap in the final quad-chopped image makes it more suitable for smaller targets such as point sources. Chop-nod may be more appropriate for targets which fill more than 1/4 of the detector area.
3. Imperfect registration of chop-nod images will compromise the PSF of the final image, since chop-nod does not involve any shifting of part of the final image with respect to another.